Q: 1 The Boolean expression x(x+y) is equal to
x
y
xy
None of the above
[ Option A ]
Given Boolean Expression:
=x(x+y)
=xx+xy
=x+xy
=x(1+y)
=x.1
=x
Q: 2 Write the simplified form of the Boolean expression (A+C)(AD+AD’)+AC+C?
A+C
A+C’
A’+C
A+D
[ Option A ]
Given Boolean expression:
=(A+C)(AD+AD’)+AC+C
=(A+C)(AD+AD’)+C(A+1)
=(A+C)(AD+AD’)+C.1
=(A+C)(AD+AD’)+C
=AAD+AAD’+ACD+ACD’+C
=AD+AD’+ACD+ACD’+C
=AD+AD’+C(AD+AD’+1)
=AD+AD’+C.1
=AD+AD’+C
=A(D+D’)+C
=A.1+C
=A+C
Therefore, (A+C)(AD+AD’)+AC+C = A+C
Q: 3 Assume x’ represents negation of x, the Boolean function x’y’ + xy + x’y is equivalent to?
x'+y
x+y
x+y’
x’+y’
[ Option A ]
The given Boolean expression:
= x’y’+xy+x’y
= x’y’+x’y+xy
=x’(y’+y)+xy
=x’.1+xy
=x’+xy
=(x’+x)(x’+y)
=1.(x’+y)
=x’+y
Therefore, x’y’+xy+x’y = x’+y
Q: 4 The Boolean expression A + BC equals
(A’+B)(A’+C)
(A+B)(A’+C)
(A+B)(A+C)
None of the above
[ Option C ]
Truth Table Confirmation:
| A | B | C | BC | A+B.C | (A+B) | (A+C) | (A+B).(A+C) |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Q: 5 The number of minterms in a n variable truth table is?
n2
(n-1)2
2n
2n-1
[ Option C ]
The number of minterms in an n-variable truth table is 2n. This is because each Boolean variable can have two possible values, 0 or 1. When there are n variables, the total number of possible input combinations is 2n. Each unique input combination corresponds to exactly one minterm. Therefore, an n-variable truth table contains 2n minterms.
Q: 6 Which one of the following Boolean algebraic rules is correct?
A.A’=1
A+AB=A+B
A+A’B=A+B
A(A+B)=B
[ Option C ]
Q: 7 In K-Map, those groups which cover at least one minterm that can't be covered by any other prime implicant is called –
Prime Implicit
Essential Prime Implicit
Redundant Prime Implicit
Selective Prime Implicit
[ Option B ]
Q: 8 Simplified Boolean function of Boolean function F=A’C+A’B+AB’C+BC is
F=C+A’B
F=A’B+B’C
F=BC+A’B
None of the above
[ Option A ]
Given Expression:
F=A’C+A’B+AB’C+BC
F=A’C+A’B+C(B+AB’)
F=A’C+A’B+C((A+B)(B+B’))
F=A’C+A’B+C(A+B)
F=A’C+A’B+AC+BC
F=A’C+AC+A’B+BC
F=C(A’+A)+A’B+BC
F=C+BC+A’B
F=C(1+B)+A’B
F=C+A’B
Q: 9 What is the minimal form of Karnaugh Map shown below? (Assume that x denotes a don’t care term)
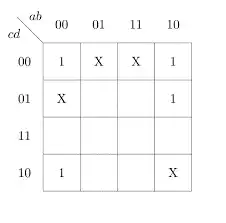
b’d’
b’d’+b’c’
b’d’+a’d’c’d’
b’d’+b’c’+c’d’
[ Option B ]
In the given K-map, two quads are formed. The first quad includes minterms 0, 2 and 8 and the don’t care terms 10, while the second quad includes minterms 0, 2 and 6 and the don’t care terms 4.
Quad 1 : a’b’c’d’+ab’c’d’+a’b’cd’+ab’cd’ : b’d’
Quad 2 : a’b’c’d’+a’b’c’d+ab’c’d’+ab’c’d : b’c’
Therefore, the minimal form is b’d’+b’c’.
Q: 10 The Boolean expression X.(X+Y) is same as:
X.(1+Y)
X
X.1
All of these
[ Option B ]
Given boolean expression:
=X.(X+Y)
=X.X+X.Y
=X+X.Y
=X(1+Y)
=X.1
=X
So, X.(X+Y) = X
Q: 11 Which of the following is equivalent to the expression ((X+Y)'+Z')'.
(X'+Y')Z
(X+Y)Z'
(X'+Y')Z'
(X+Y)Z
[ Option D ]
Given Boolean expression,
=((X+Y)’+Z’)’
=(X+Y)’’.Z’’
=(X+Y).Z
So, ((X+Y)’+Z’)’ = (X+Y).Z
Q: 12 What is the purpose of the “don’t care” condition in digital logic?
To indicate that the value of a variable does not affect the output
To prioritize certain inputs over others
To ensure that all possible input combinations are covered in truth tables
None of the above
[ Option A ]
In digital logic, a “don’t care” condition indicates that the value of a particular input does not affect the final output of the circuit. These conditions are used during simplification of Boolean expressions or Karnaugh maps (K-maps).
Because the output does not depend on certain inputs, we are free to treat those inputs as either 0 or 1, whichever helps produce the simplest possible expression.
“Don’t care” conditions do not prioritize inputs nor ensure completeness of truth tables, instead, they are a tool for simplification.
Q: 13 The minimum number of gates needed to implement the following Boolean function.
f(x,y,z) = z(x+y)+((z’+x+y)(x’+y’))’
2
3
4
5
[ Option A ]
f(x,y,z) = z(x+y)+((z’+x+y)(x’+y’))’
f(x,y,z) = z(x+y)+((x’z’+y’z’+xx’+xy’+yy’))’
f(x,y,z) = z(x+y)+(x’z’+y’z’+xy’)’
f(x,y,z) = z(x+y)+((x’z’)’.(y’z’)’.(xy’)’)
f(x,y,z) = z(x+y)+((x’’+z’’).(y’’+z’’).(x’+y’’))
f(x,y,z) = z(x+y)+((x+z).(y+z).(x’+y))
f(x,y,z) = z(x+y)+((xy+xz+yz+zz).(x’+y))
f(x,y,z) = z(x+y)+((xy+xz+yz+z).(x’+y))
f(x,y,z) = z(x+y)+((xy+z).(x’+y))
f(x,y,z) = z(x+y)+(xyx’+xyy+x’z+yz)
f(x,y,z) = z(x+y)+(xy+x’z+yz)
f(x,y,z) = xz+yz+xy+x’z+yz
f(x,y,z) = xz+x’z+xy+yz
f(x,y,z) = z(x+x’+y)+xy
f(x,y,z) = z.1+xy
f(x,y,z) = z+xy
So, there is only 2 gates required one AND and one OR gate.
Q: 14 How many Boolean expressions can be formed with 3 Boolean variables?
16
1024
32
256
[ Option D ]
If there are n Boolean variables, then:
Here the number of Boolean variable is 3, so:
Q: 15 Which of these is a dual of A+(B.C) = (A+B) . (A+C) ?
A.(B+C) = (A.B) + (A.C)
A+ (B+C) = (A+B) +C
A. (B.C) = (A.B) .C
All of the above
[ Option A ]
Principle of Duality says, every algebraic expression remains valid if you interchange:
(1) AND (·) with OR (+)
(2) 0 with 1
🧠 In simple words, for every Boolean law or expression, there exists a dual expression that is also valid.
E.g.:
(1) A + 0 = A, its Dual is A . 1 = A
(2) A + A =A, its Dual is A . A = A
(3) A . 0 = 0, its Dual is A + 1 =1
Q: 16 The Boolean expression A+BC equals
(A’+B)(A’+C)
(A+B)(A’+C)
(A+B)(A+C)
More than one of the above
[ Option C ]
Apply distributive law.
Q: 17 The Boolean expression x+x’y equals
x+y
x+xy
y+yx
None of the above
[ Option A ]
Given Boolean Expression:
x+x’y
To simplify the expression, we apply Boolean algebra rules:
(x+x’) (x+y) Apply Distributive Law.
(1)(x + y) Because x+x’=1
x+y Because A.1=A
So, x+x’y = x+y
Q: 19 Derive the Boolean expression for the logic circuit shown below:
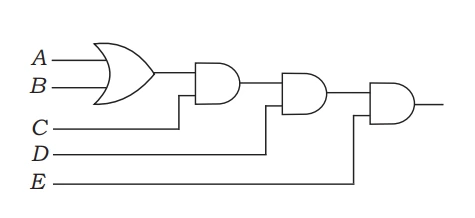
C(A+B)DE
[C(A+B)D+E’]
[[C(A+B)D]E’]
None of the above
[ Option A ]
Q: 20 In two-valued Boolean algebra, the maximum number of Boolean functions for two variables will be
4
8
12
16
[ Option D ]
In two-valued Boolean algebra, for two variables, the number of possible Boolean functions is given by the formula 2(2ⁿ). Where n is the number of variables. Here n=2, So, 2(22) = 24 = 16. Therefore, the maximum number of Boolean functions for two variables is 16.
Q: 21 For Boolean function, f(A, B, C) = Σ m(0, 1, 3, 5) + Σ d(2, 7) , the minimized sum-of-product equation is : (using K-Map)
A' + C'
A' + B' + C'
A' . B' . C'
C + A'
[ Option D ]
Q: 22 The Boolean expression AB+AB’+A’C+AC is independent of Boolean variable?
A
B
C
A'
[ Option B ]
The given Boolean expression is AB + AB’ + A’C + AC. To determine which variable it is independent of, we simplify the expression.
First, we combine AB + AB’, which simplifies to A(B + B’). Since B + B’ = 1, this becomes A. Substituting this back, the expression becomes A + A’C + AC.
Next, we combine A + AC, which simplifies to A(1 + C) = A, because anything ORed with 1 is 1. So the expression now becomes A + A’C.
In this simplified form, we can see that the expression still contains A and C, but B no longer appears. Therefore, the Boolean expression is independent of variable B.
Q: 23 The minimized expression for a 4-variables logic function, f(A, B, C, D) = Σm(0, 1, 2, 3, 5, 7, 8, 9, 11, 14) , using K-Map is
(Ā + B + C̅ + D) (Ā + B̅ + C) (Ā + B̅ + D̅) (A + B̅ + D)
ABCD̅ + B̅C̅ + B̅D + A̅D + A̅B̅
B̅ + A C̅ + A̅ C D
A̅B̅C̅D + BC + BD̅ + AD̅ + AB̅
[ Option B ]
Q: 24 Consider the following Boolean expression for F:
F(P,Q,R,S) = PQ + P’QR + P’QR’S
The minimum sum of products form of F is?
PQ+QR+QS
P+Q+R+S
P’+Q’+R’+S’
P’R+P’R’S+P
[ Option A ]
The given boolean expression F(P,Q,R,S) = PQ + P’QR + P’QR’S can be solved by either using K-Map or boolean theorem.
= PQ+P’QR+P’QR’S
=Q(P+P’R)+P’QR’S
=Q(P+R)+P’QR’S
=PQ+QR+P’QR’S
=PQ+Q(R+P’R’S)
=PQ+Q(R+P’S)
=PQ+QR+P’QS
=QR+Q(P+P’S)
=QR+Q(P+S)
=QR+PQ+QS
=PQ+QR+QS
Therefore, PQ+P’QR+P’QR’S = PQ+QR+QS
Q: 25 According to the duality theorem, the dual of the Boolean expression A+0=A is:
A.0=0
A+1=A
A.A=A
A.1=A
[ Option D ]
Principle of Duality says, every algebraic expression remains valid if you interchange:
1) AND (·) with OR (+)
2) 0 with 1
In simple words, for every Boolean law or expression, there exists a dual expression that is also valid. E.g.:
1) A + 0 = A, its Dual is A . 1 = A
2) A + A =A, its Dual is A . A = A
3) A . 0 = 0, its Dual is A + 1 =1
Q: 26 A tautology is a Boolean formula that is always true. Which of the following is a tautology?
x
(x+x’)y
x+y’+x’
(xy)+x’
[ Option C ]
In option (A), The value of x depends on the input. If x=0, the expression is 0 and if x=1, the expression is 1. Since it is not always true, this is not a tautology.
In option (B), (x+x′)y, we know that x+x′=1. So, the expression becomes 1.y=y. The value now depends on y. If y=0, the output is 0. Hence, this is not always true and not a tautology.
In option (C), x+y’+x’, we know that x+x′=1. So, the expression becomes 1+y’=1. This result is always 1, irrespective of the value of y. Therefore, this expression is always true and is a tautology.
In option (D), (xy)+x’, if x=1, the expression becomes y+0=y, which can be 0 or 1 and if x=0, the expression becomes 0+1=1. Since the result is not always 1, this is not a tautology.
Q: 27 The expression Y=AB+BC+AC show the ____________ operations.
EX-OR
SOP
POS
More than one of the above
[ Option B ]
The given Boolean expression is Y=AB+BC+AC. Here, each term (AB, BC, AC) is a product term (logical AND). These product terms are then summed together (logical OR). This format of “logical sum of several product terms” is known as Sum of Products (SOP).
Q: 28 The function AB’C + A’BC + ABC’ + A’B’C + AB’C’ is equivalent to
AC’ + AB + A’C
A’C + BC + A’C’
AC’ + A’C + B’C’
AB’ + A’C + AC’
[ Option D ]
F = AB’C+A’BC+ABC’+A’B’C+AB’C’
F = AB’C+AB’C’+A’BC+A’B’C+ABC’
F = AB’(C+C’)+A’C(B+B’)+ABC’
F = AB’+A’C+ABC’
F = AB’+ABC’+A’C
F = A(B’+BC’)+A’C
F = A(B’+C’)+A’C
F = AB’+AC’+A’C
Q: 29 The switching expression corresponding to f(A,B,C,D) =Σ(1,4,5,9,11,12) is:
BC'D'+A'C'D+AB'D
ABC'+ACD+B'C'D
ACD'+A'BC'+AC'D'
A'BC+ACD+BCD'
[ Option A ]
The symbol Σ (Sigma) means the function is expressed as a sum of minterms.
Since there are four variables, we use a 4-variable K-map. The variables AB represent the rows and CD represent the columns, arranged in gray code order (00, 01, 11, 10). We place 1s in the cells corresponding to minterms 1, 4, 5, 9, 11, and 12.
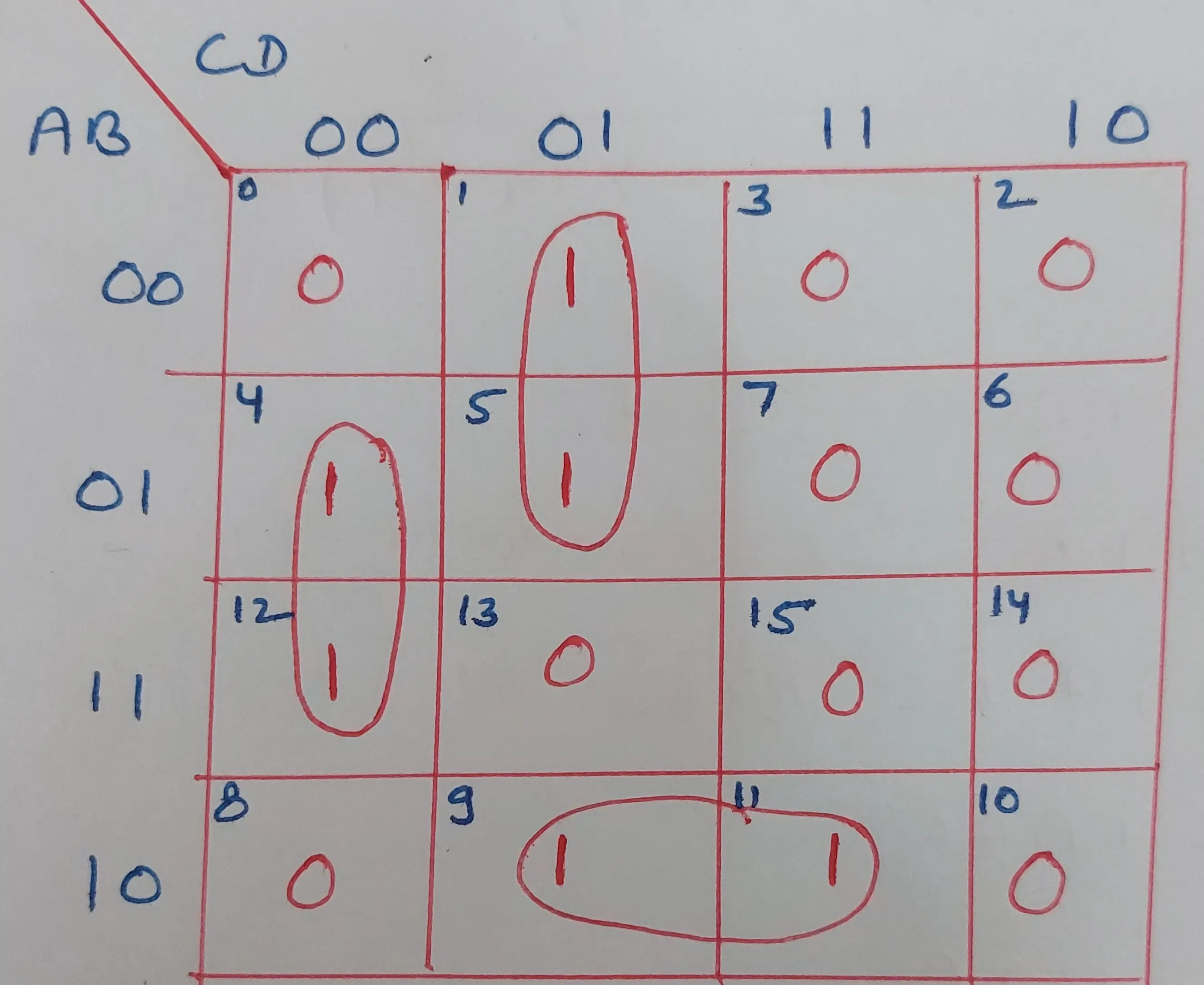
Here we found 3 pairs, pair one using minterm 1 and 5, pair second using minterm 4 and 12 and pair third using minterm 9 and 11.
Pair 1 : A’B’C’D + A’BC’D = A’C’D
Pair 2 : A’BC’D’ + ABC’D’ = BC’D’
Pair 3 : AB’C’D + AB’CD = AB’D
Therefore, F(A,B,C,D) = A’C’D + BC’D’ + AB’D
Q: 30 The number of terms in the product of sum canonical of ((x1+x2)(x3+x4)')' is?
7
8
9
10
[ Option C ]
Given boolean expression,
=((x1+x2)(x3x4)’)’
=(x1+x2)’+(x3x4)’’
=x1’x2’+x3x4
Now, construct the truth table for this simplified Boolean expression. In the truth table, output ‘1’ represents the minterms (Sum of Products), and output ‘0’ represents the maxterms (Product of Sums).
| INPUT | OUTPUT | |||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | x1' | x2' | x1'x2' | x3x4 | Y= x1’ x2’+ x3x4 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
In the final output column, the total number of 1’s is 7 and the total number of 0’s is 9. Therefore, the number of Sum of Product (SOP) terms is 7, and the number of Product of Sum (POS) terms is 9.
Q: 31 Consider x and y be some Boolean variables, “+” denotes the OR operation and “.” Denotes the AND operation. What will be the simplified form of the Boolean expression:
x.(x+y)?
y
1
0
x
[ Option D ]
Given Boolean expression:
=x.(x+y)
=x.x+x.y
=x+x.y
=x(1+y)
=x.1
=x
So, x.(x+y) = x
Q: 32 Boolean algebra can be used
for designing the digital computers
in building logic symbols
in circuit theory
More than one of the above
[ Option D ]
Boolean algebra is the mathematical foundation of digital electronics. It deals with binary variables and logical operations, which makes it very useful in several areas.
Q: 33 The simplified form of the Boolean expression (X+Y+XY)(X+Z) is
XY+YZ
X+YZ
XZ+Y
None of the above
[ Option B ]
Given Boolean Expression:
=(X+Y+XY)(X+Z)
=(Y+X(1+Y))(X+Z)
=(Y+X.1)(X+Z)
=(Y+X)(X+Z)
=XY+YZ+XX+XZ
=X+XY+XZ+YZ
=X(1+Y+Z)+YZ
=X.1+YZ
=X+YZ
Q: 34 Which term is redundant in the expression AB+A’C+BC is?
BC
A’C
AB
None of these
[ Option A ]
According to the Consensus Theorem, the term BC is the redundant term and can be removed without changing the value of the Boolean expression.
Consensus Theorem : AB+A′C+BC = AB+A′C
We can also verify this using a Truth Table or K-Map for extra clarity.
USING K-MAP:
For a K-map, we always require either a collection of minterms or a collection of maxterms. Since the given expression is in Sum of Products (SOP) form, we first convert it into Standard SOP (SSOP), that is, a collection of minterms.
SOP : AB+A’C+BC
SSOP : AB.1+A’C.1+BC.1
=AB(C+C’)+A’C(B+B’)+BC(A+A’)
=ABC+ABC’+A’BC+A’B’C+ABC+A’BC
=ABC+ABC’+A’BC+A’B’C (Remove redundant terms)
In a minterm, each variable appears exactly once, an uncomplemented variable indicates a value of 1, whereas a complemented variable indicates a value of 0.
Therefore,
ABC=111 = 7 = m7
ABC’=110 = 6 = m6
A’BC=011 = 3 = m3
A’B’C=001 = 1 = m1
F(A,B,C) = Σ(1,3,6,7)
Since there are three variables, we use a 3-variable K-map. The variables A represent the rows and BC represent the columns, arranged in gray code order (00, 01, 11, 10). We place 1s in the cells corresponding to minterms 1, 3, 6 and 7.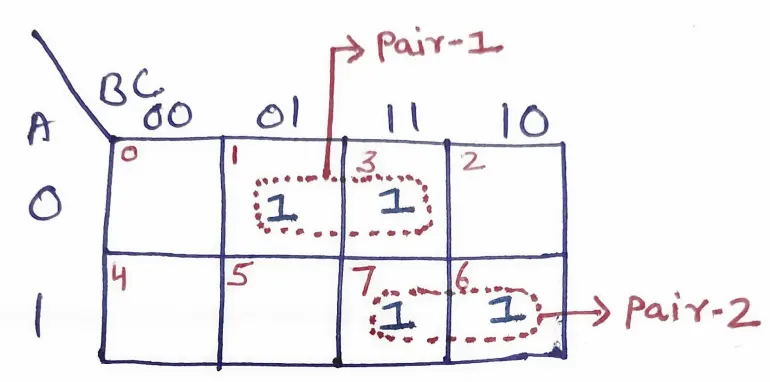
In this K-map, two pairs are formed. The first pair includes minterms 1 and 3, while the second pair includes minterms 6 and 7.
Pair 1 : A’B’C+A’BC = A’C
Pair 2 : ABC+ABC’ = AB
F(A,B,C) = A’C+AB
Therefore, BC is the redundant (consensus) term.
USING TRUTH TABLE:
F=AB+A′C+BC
| A | B | C | AB | A' | A′C | BC | AB+A′C | AB+A′C+BC |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
The output column AB+A′C and AB+A′C+BC are identical for all input combinations. So, adding or removing the term BC does not change the final output. Therefore, BC is the redundant (consensus) term.
Q: 35 In two-valued Boolean algebra, the maximum number of Boolean functions for two variables will be
8
12
16
None of the above
[ Option C ]
In two-valued Boolean algebra, each variable can take only two values: 0 or 1. When we have two Boolean variables, there are four possible input combinations, (0,0), (0,1), (1,0) and (1,1).
For each of these combinations, a Boolean function can output either 0 or 1. Therefore, the total number of possible Boolean functions is calculated by raising 2 to the power of the number of input combinations. Since there are four combinations, the number of functions becomes 24=16.
Q: 37 Consider the following minterm expression for F:
F(P,Q,R,S) = Σ(0,2,5,7,8,10,13,15)
The minterm 2, 7, 8 and 13 are do not care terms. The minimal sum of product form for F is?
QS'+Q'S
Q'S'+QS
Q'R'S'+Q'RS'+QR'S+QRS
P'Q'S'+P'QS+PQS+PQ'S'
[ Option B ]
The symbol Σ (Sigma) means the function is expressed as a sum of minterms.
Since there are four variables, we use a 4-variable K-map. The variables PQ represent the rows and RS represent the columns, arranged in gray code order (00, 01, 11, 10). We place 1s in the cells corresponding to minterms 0, 2, 5, 7, 8, 10, 13 and15.
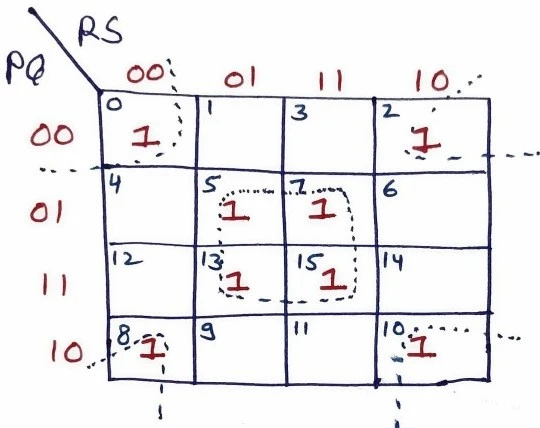
In this K-map, two quads are formed. The first quad includes minterms 0 and 10 and the don’t care terms 2 and 8, while the second quad includes minterms 5 and 15 and the don’t care terms 7 and 13.
Quad 1 : P’Q’R’S’ + P’Q’RS’ + PQ’R’S’ + PQ’RS’ : Q’S’
Quad 2 : P’QR’S + P’QRS + PQR’S + PQRS : QS
Therefore, F(P,Q,R,S) = Q’S’ + QS
Q: 38 The Boolean expression AB+AB’+A’C+AC is independent of Boolean variable
A
B
C
None of the above
[ Option B ]
Given Boolean Expression:
=AB+AB’+A’C+AC
=A(B+B’)+C(A’+A)
=A.1+C.1
=A+C
The simplified expression A+C contains variables A and C, but does not contain B. Therefore, the Boolean expression is independent of variable B.
Q: 41 Which one of the following is not a valid rule of Boolean algebra?
A+1 = 1
A = A’
A.A = A
A+0 = A
[ Option B ]
The statement A=A’ means a variable is equal to its complement. This is not possible in Boolean algebra because a variable and its complement always have opposite values.
Truth Table Verification:
| A | A' | A+1=1 | A.A=A | A+0=A |
|---|---|---|---|---|
| 0 | 1 | 0+1=1 | 0.0=0 | 0+0=0 |
| 1 | 0 | 1+1=1 | 1.1=1 | 1+0=1 |
Q: 42 The Boolean expression x+xy will be equal to
x
y
x+y
None of the above
[ Option A ]
Given Boolean Expression:
=x+xy
=x(1+y)
=x.1
=x
Q: 43 Simplified form of a Boolean function F(X,Y,Z) = Σm(0,2,4,5,6) is:
Z'X+XY'
Z'+XY'
Y'Z'+XY'
None of these
[ Option B ]
The symbol Σ (Sigma) means the function is expressed as a sum of minterms.
Since there are three variables, we use a 3-variable K-map. The variables X represent the rows and YZ represent the columns, arranged in gray code order (00, 01, 11, 10). We place 1s in the cells corresponding to minterms 0, 2, 4, 5 and 6.
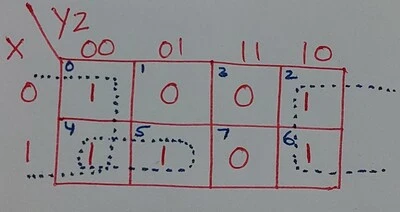
Here we found 1 quad using minterms 0, 2, 4 and 6 and 1 pair using minterms 4 and 5.
Quad : X’Y’Z’ + XY’Z’ + X’YZ’ + XYZ’ = Z’
Pair : XY’Z’ + XY’Z = XY’
Therefore, F(X,Y,Z) = Z’+XY’
Q: 44 Which of the following is equivalent to the Boolean expression
(X+Y)(X+Y’)(X’+Y)
XY
XY’
X’Y
X’Y’
[ Option A ]
Given Boolean expression:
=(X+Y)(X+Y’)(X’+Y)
=(XX+XY’+XY+YY’)(X’+Y)
=(X+XY’+XY+0)(X’+Y)
=(X+XY’+XY)(X’+Y)
=X(1+Y’+Y)(X’+Y)
=(X.1)(X’+Y)
=X(X’+Y)
=XX’+XY
=0+XY
=XY
Therefore, (X+Y)(X+Y’)(X’+Y) = XY
Q: 45 What are the canonical forms of Boolean expressions?
OR and XOR
NOR and XNOR
SOM and POM
More than one of the above
[ Option C ]
The canonical forms of Boolean expressions are:
These forms represent Boolean functions in standard forms using all variables in each term.
Note:
Q: 46 If x is a Boolean variable, then (((x’)’)’)’ will be
x'
x
x+x’
More than one of the above
[ Option B ]
Evaluate the expression step by step using the double-negation (complement) rule (x’)’=x.
Thank you so much for taking the time to read my Computer Science MCQs section carefully. Your support and interest mean a lot, and I truly appreciate you being part of this journey. Stay connected for more insights and updates! If you'd like to explore more tutorials and insights, check out my YouTube channel.
Don’t forget to subscribe and stay connected for future updates.