Q: 1 Consider the following statement:
S1: Ternary search is more efficient than binary search for finding an element in a sorted array.
S2: Worst case deletion and insertion in an AVL tree have same complexity.
S1 is correct, S2 is not
S2 is correct, S1 is not
Both are correct
Both are incorrect
[ Option B ]
Statement S1: Ternary search divides the array into three parts, while binary search divides it into two parts. Although ternary search reduces the search space into more parts, it requires more comparisons per step than binary search. As a result, binary search is generally more efficient for finding an element in a sorted array. Hence, S1 is incorrect.
Statement S2: In an AVL tree, both insertion and deletion operations may require rebalancing the tree. In the worst case, both operations take O(log n) time because the height of an AVL tree is always logarithmic. Hence, S2 is correct.
Q: 2 How many edges does a spanning tree of a graph with N vertices have?
N
N-1
N(N-1)/2
None of the above
[ Option B ]
A spanning tree is a subgraph of a connected graph that includes all the vertices but only enough edges to keep the graph connected without forming any cycles.
Q: 3 In a binary search tree, which subtree of a node contains elements that are greater than the node’s value?
Left Subtree
Right Subtree
Both Subtrees
None of the above
[ Option B ]
A Binary Search Tree (BST) is a special type of binary tree where the arrangement of elements follows a strict rule:
This property allows fast searching, because at each step, the tree decides whether to go left (for smaller values) or right (for larger values).
Q: 4 If we implement heap as maximum heap, adding a new node of value 15 to the left most node of right subtree, what value will be at leaf nodes of the right subtree of the heap?
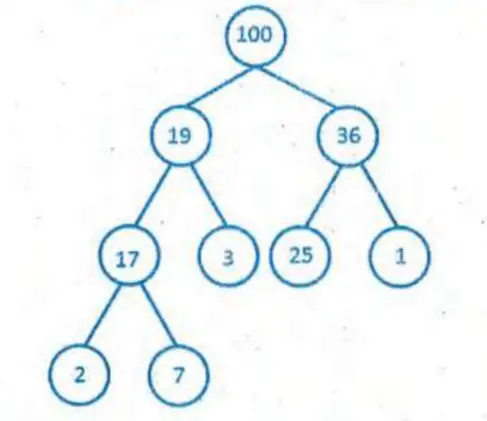
15 and 1
25 and 1
3 and 1
2 and 3
[ Option A ]
Q: 5 The preorder traversal of a binary search tree is 15, 10, 12, 11, 20, 18, 16, 19. Which one of the following is the postorder traversal of the tree?
20, 19, 18, 16, 15, 12, 11, 10
11, 12, 10, 16, 19, 18, 20, 15
19, 16, 18, 20, 11, 12, 10, 15
None of the above
[ Option B ]
A Binary Search Tree (BST) is a special type of binary tree that is designed to allow fast searching, insertion, and deletion of data. In BST:
The preorder traversal sequence is given and in case of BST, the inorder traversal always sorts the tree nodes into ascending order.
Preorder : 15, 10, 12, 11, 20, 18, 16, 19
Inorder : 10, 11, 12, 15, 16, 18, 19, 20
WHEN PREORDER AND INORDER TRAVERSAL GIVEN:
So, the resultant BST is:
15
/
10 20
/
12 18
/ /
11 16 19
Final Postorder traversal sequence is 11, 12, 10, 16, 19, 18, 20, 15
Q: 6 In a balanced binary tree, the height of two sub-trees of every node can not differ by more than
2
1
0
None of the above
[ Option B ]
A binary tree is a hierarchical data structure in which each node can have at most two children, called the left child and the right child.
Now, some binary trees can grow in an uneven manner. For example, all nodes may keep inserting to the left side only. This makes the tree skewed, and searching becomes slow. To avoid this, we use a balanced binary tree.
A Balanced Binary Tree is a special type of binary tree in which the height (depth) of the left and right subtrees of every node is kept nearly equal.
Height of left subtree and right subtree differ by 0 or 1 only.
This condition must hold at every node in the tree, not just the root.
So, in a balanced binary tree (AVL Tree), the difference between the heights of the left and right subtree of any node is allowed to be at most 1.
Q: 7 Which one of the following techniques is not used in the binary tree?
Randomized traversal
Preorder traversal
Postorder traversal
More than one of the above
[ Option A ]
A binary tree is commonly traversed using three standard tree traversal techniques:
These methods are systematic and widely used in all tree-related algorithms.
Q: 8 The preorder traversal of a Binary Search Tree (BST) is 100, 50, 20, 30, 60, 55, 150, 130, 140, 180, 170. What would be its postorder traversal?
20, 30, 55, 60, 50, 130, 140, 180, 170, 150, 100
20, 30, 55, 60, 50, 140, 130, 180, 170, 150, 100
30, 20, 55, 60, 50, 140, 130, 170, 180, 150, 100
30, 20, 60, 55, 50, 130, 140, 180, 170, 150, 100
[ Option C ]
As we know, inorder traversal of BST is in sorted order. So,
Inorder Traversal : 20, 30, 50, 55, 60, 100, 130, 140, 150, 170, 180
Preorder Traversal : 100, 50, 20, 30, 60, 55, 150, 130, 140, 180, 170
With Inorder and Preorder, unique BST can be determined.
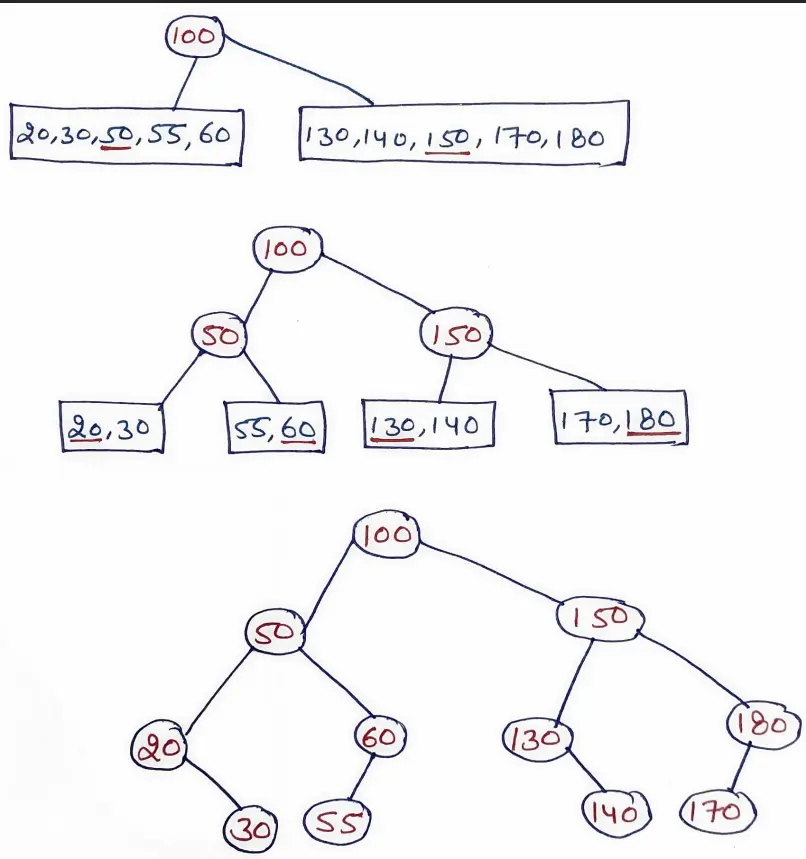
Using the above constructed BST, the postorder traversal sequence is:
Postorder Traversal : 30, 20, 55, 60, 50, 140, 130, 170, 180, 150, 100
Q: 9 Let QUSVPTR is in-order traversal and UVSQTRP is post-order traversal of a binary tree T. Which of the following is pre-order traversal of the binary tree T?
PUQSVRT
UVRTPQS
SQPRTVU
PQSUVRT
[ Option D ]
Q: 10 Which of the following options is not true about the binary search tree?
The value of the left child should be less than the root node.
The value of the right child should be greater than the root node.
The left and right subtrees should also be a binary search tree.
None of the above
[ Option D ]
A Binary Search Tree (BST) is a binary tree where nodes follow a strict ordering rule for efficient searching, insertion, and deletion. Each node has at most two children.
BST Rule:
Q: 11 Let a BST is constructed by inputting an ordered list [33, 45, 2, 91, 47, 95] from left to right. Which of the following pair of elements will be on the last level of the BST?
47, 91
47, 95
2, 95
91, 95
[ Option B ]
33
/
2 45
91
/
47 95
Q: 12 Which of the following graphs are trees?
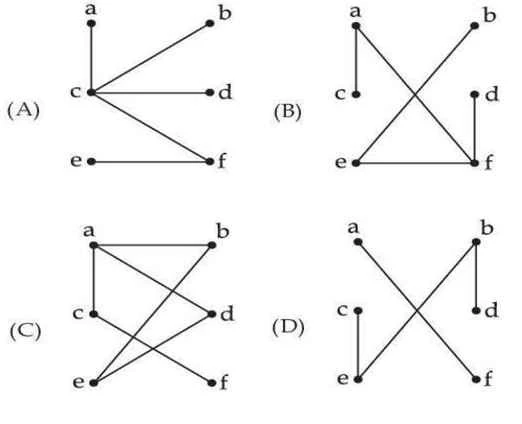
(A) and (B) only
(A), (B) and (D) only
(A) and (D) only
(A), (B), (C) and (D) only
[ Option A ]
Here,
(a) and (b) are trees.
(c) is not a tree because adeb form a graph
(d) It is not hierarchical so that is why not a tree.
Q: 13 Which of the following TREE traversal technique is NOT based on Depth First Search (DFS)?
Level Order Traversal
Preorder Traversal
Inorder Traversal
Postorder Traversal
[ Option A ]
The Level Order Traversal also known as Breadth First Search (BFS) while other three are DFS.
Q: 14 Which of the following algorithms uses the greedy approach to find a Minimum Spanning Tree (MST)?
Bellman-Ford Algorithm
Kruskal’s and Prim’s Algorithm
Floyd-Warshall Algorithm
Dijkstra’s Algorithm
[ Option B ]
A Minimum Spanning Tree (MST) is a subset of the edges of a connected, weighted graph that:
Algorithms for MST:
Bonus:
Q: 15 What is true about the height h of a B-tree with n keys (n ≥ 1) and minimum degree t ≥ 2 ?
h ≤ logt(n) + 1
h ≤ logt((n + 1) / 2)
h ≤ logt(n-1)
h ≤ log2(n)
[ Option B ]
Q: 16 How many distinct binary search trees can be created out of 4 distinct keys?
8
24
14
None of the above
[ Option C ]
When number of node N is given then how many total numbers of possible binary trees can be drawn. This can be calculated using Catalan number. Cn=(2n)!/(n+1)!n!, where, n is number of nodes.
When n=4.
C4 = (2*4)!/(4+1)!*4!
C4 = 8!/5!*4!
C4 = 8*7*6*5!/5!*4*3*2*1
C4 = 336/24
C4 = 14
Q: 17 Which one of the following techniques is not used in the binary tree?
Preorder traversal
Inorder traversal
Postorder traversal
None of the above
[ Option D ]
A binary tree is a hierarchical data structure in which each node has at most two children. To process or visit all nodes of a binary tree, several traversal techniques are used:
All three are standard and commonly used techniques for binary tree traversal.
Q: 18 Consider the given binary search tree, if the root node will be deleted, the new root can be-
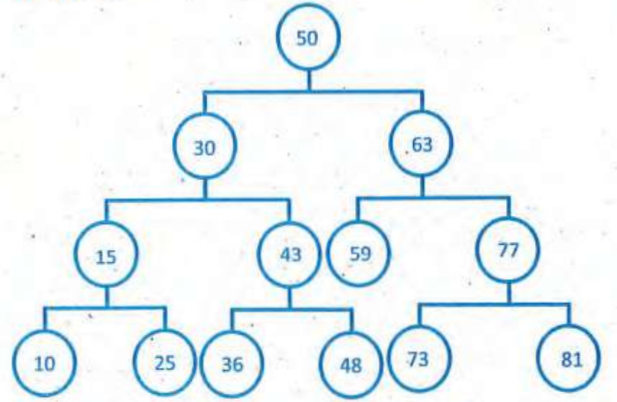
43 or 48
63 or 81
48 or 59
30 or 63
[ Option C ]
Q: 19 What will be post order traversal of a binary Tree T, if preorder and inorder traversals of T are given by ABCDEF and BADCFE respectively?
BDFECA
BCFDEA
BFDECA
BEFDCA
[ Option A ]
In a tree data structure, there are three primary types of traversal sequences used to visit all the nodes systematically: Preorder, Inorder, and Postorder traversal.
So,
(1) Preorder Traversal: Root → Left → Right
(2) Inorder Traversal: Left → Root → Right
(3) Postorder Traversal: Left → Right → Root
The preorder traversal of the tree is ABCDEF, which means the root of the tree is A. Looking at the inorder traversal BADCFE, we see that A splits the tree into a left subtree (B) and a right subtree (DCFE). Thus, B is the left child of A, and the rest of the nodes (DCFE) belong to the right subtree.
In the right subtree, the preorder sequence is CDEF, so the root here is C. From the inorder sequence DCFE, the node C splits the subtree into D on the left and FE on the right. For the FE part, preorder tells us the root is E, and inorder (FE) shows that F is on the left of E. This gives the right subtree structure: C has left child D and right child E, with E having left child F.
Now, constructing the postorder traversal: start with the left subtree of A which is B, then the right subtree rooted at C. For C, its left subtree gives D, and its right subtree rooted at E gives F followed by E. After these, we add the root C. Finally, we append the overall root A. Putting this together, the Postorder is B D F E C A.
Q: 20 Which best describes how Kruskal’s algorithm constructs a Minimum Spanning Tree (MST)?
Adds edges in increasing order of weight while avoiding cycles.
Adds the smallest edge that connects a visited vertex to an unvisited one.
Grows the MST by adding the maximum weight edge from a starting node.
Selects a root and grows the MST by always choosing the closest neighbour.
[ Option A ]
Kruskal’s algorithm is a greedy algorithm used to find the Minimum Spanning Tree (MST) of a connected, weighted graph. It works by sorting all the edges of the graph in non-decreasing order of their weights. Then, it iteratively adds the smallest edge to the MST, provided that adding the edge does not create a cycle in the growing tree.
The algorithm continues until the MST has exactly V−1 edges, where V is the number of vertices.
Unlike Prim’s algorithm, which grows the MST from a starting vertex, Kruskal’s algorithm builds the MST by focusing on edges first, ensuring the final tree has the minimum total weight.
Must Know:
Non-decreasing order of their weight means the edges are arranged from smallest weight to largest weight, but equal weights are allowed to appear next to each other. For example, if the edge weights are [6, 2, 9, 4, 2], then sorted in non-decreasing order they become [2, 2, 4, 6, 9].
Thank you so much for taking the time to read my Computer Science MCQs section carefully. Your support and interest mean a lot, and I truly appreciate you being part of this journey. Stay connected for more insights and updates! If you'd like to explore more tutorials and insights, check out my YouTube channel.
Don’t forget to subscribe and stay connected for future updates.